El informe de las pruebas PISA 2022, centradas en evaluar el rendimiento matemático, ha puesto sobre la mesa un importante descenso del nivel de los estudiantes de secundaria. Estos resultados, lejos de desalentar, pueden servir de motivación para reflexionar y mejorar la enseñanza de las matemáticas.
Para comprender los resultados del Informe PISA es necesario saber cómo son sus pruebas y cómo se evalúan. Estos exámenes están diseñados para plasmar el nivel de competencia matemática de los alumnos de 15 años de secundaria, competencia que PISA define como “la capacidad de razonar matemáticamente y de formular, emplear e interpretar las matemáticas para resolver problemas en una variedad de contextos de la vida real”.
Seguro que has oído hablar mucho de las competencias. La ley de educación LOMLOE las ubica en el centro del aprendizaje, y es a partir de 8 competencias clave que se desgranan las competencias específicas del área, los saberes y los contenidos. ¡Pero no son relevantes solo en España! Las competencias son fundamentales en todas las estrategias educativas internacionales, siempre con el objetivo de formar a los alumnos para que sean ciudadanos capaces y resolutivos.
Un alumno competente es aquel capaz de hacer frente a los problemas de su día a día y los retos del siglo XXI. Para lograrlo, la competencia matemática es una de las más esenciales.
¿Qué han de saber los alumnos para obtener buenos resultados en las pruebas PISA?
Desde la OCDE (Organización para la Cooperación y el Desarrollo Económicos) se diseñan las pruebas PISA con preguntas competenciales que no se solucionan únicamente ejecutando algoritmos; se pide a los alumnos que reflexionen y apliquen estrategias para resolver las situaciones matemáticas que se proponen.
Esta es una de las características clave: los problemas contextualizados evalúan diferentes procesos de razonamiento matemático, de menor a mayor complejidad cognitiva. Así, mediante la resolución de problemas, se valora la capacidad de conectar los saberes matemáticos y de poner en práctica las habilidades y procesos necesarios para resolver la situación contextualizada de la manera más eficaz posible.
Niveles de rendimiento del Informe PISA
De la construcción de las preguntas competenciales, se deriva la capacidad de las pruebas PISA de medir el nivel de competencia de los alumnos. Se estipulan 8 niveles de rendimiento, que van desde el reconocimiento de la información y aplicación de algoritmos sencillos hasta la capacidad de aplicar estrategias y desarrollar el pensamiento crítico en contextos matemáticos:
- Nivel 1c. Resolver preguntas en contextos fáciles y con toda la información necesaria, siguiendo una instrucción clara y de un solo paso u operación.
- Nivel 1b. Resolver preguntas en contextos sencillos y con toda la información en una representación, reconociendo si hay información irrelevante y haciendo cálculos simples con números enteros.
- Nivel 1a. Resolver preguntas en contextos sencillos, con toda la información en formatos conocidos y dos fuentes. Procedimientos fáciles, mínima síntesis de información y aplicación de algoritmos elementales, fórmulas o procedimientos.
- Nivel 2. Reconocer situaciones que requieren diseñar estrategias para resolver el problema. Recabar información de varias fuentes con modelos de representación algo complejos. Compresión de relaciones funcionales y razonamientos simples.
- Nivel 3. Diseñar estrategias para llegar a la solución, incluyendo toma secuencial de decisiones y flexibilidad en la comprensión. Emplear pensamiento computacional y realizar cálculos que no están claramente definidos. Uso de visualización espacial o de simulación para recoger datos. Interpretación de las fuentes y razonamiento. Porcentajes, fracciones, decimales y relaciones proporcionales.
- Nivel 4. Trabajar con modelos para problemas complejos, con dos variables, aplicando pensamiento computacional más complejo. Desarrollo de pensamiento crítico e integrar representaciones diversas de información vinculándolas con contextos cotidianos. Argumentación, razonamiento y metodología.
- Nivel 5. Elaborar y trabajar con modelos para problemas complejos y presuposiciones. Aplicar estrategias de resolución de problemas para tareas más difíciles, como experimentos. Reflexionar sobre su actividad y considerar los resultados contextualizados.
Cómo enseñar matemáticas para formar a alumnos competentes
La manera de evaluar condiciona la manera de enseñar. No podemos esperar que los alumnos alcancen los niveles más altos de competencia matemática de las pruebas PISA si no les preparamos para ello. Para conseguirlo, hay que tener en cuenta la secuenciación cíclica, la contextualización, el razonamiento y la consolidación.
Aquí van algunas orientaciones para que tus actividades de enseñanza de las matemáticas cumplan estos requisitos:
- Programa los aprendizajes respetando los principios de la didáctica de la matemática, desde infantil hasta secundaria: ir de lo simple a lo complejo, relacionar los conocimientos y saber cuáles son imprescindibles para avanzar. Una secuenciación cíclica es clave para un aprendizaje profundo y duradero.
- Diseña actividades que tengan un contexto realista en el que poder aplicar las matemáticas. No nos referimos a un problema con datos que se resuelve con un algoritmo, sino a una situación compleja y conectada con otras disciplinas, en la que se requiere las habilidades y el lenguaje matemáticos para resolverla.
- Utiliza demostraciones matemáticas para enseñar a los alumnos a razonar y probar, a hacer conexiones, comunicar y representar el conocimiento matemático. ¡Son procesos imprescindibles para ser competente en matemáticas! Para diseñar demostraciones, te recomendamos la guía Demostraciones matemáticas: una estrategia de enseñanza explícita eficaz en secundaria.
- Dedica tiempo a la consolidación de los procedimientos matemáticos básicos, fundamentales para ser competentes. A mayor dominio de los procedimientos básicos, más capacidad para afrontar los problemas complejos con seguridad.
Para mantener la coherencia, es necesario que estas características se reflejen tanto en las actividades de aprendizaje como en las de evaluación.
Así entrenamos para PISA con ONMAT: evaluación y actividades secuenciadas
Para conseguir que los alumnos alcancen el nivel más alto en rendimiento matemático, la OCDE destaca la importancia del aprendizaje acumulativo: es fundamental asentar los primeros saberes, ya que es a partir de ellos que se construyen los conocimientos futuros. ¡Sin una base sólida, todo se derrumba!
Analicemos dos actividades contextualizadas: una pregunta de PISA y una actividad de ONMAT, nuestro programa de matemáticas de secundaria, para comprender cómo enseñar para obtener buenos resultados. Para empezar, hemos de tener en cuenta que en el Informe PISA se observa la competencia matemática mediante los siguientes aspectos interrelacionados:
- Conocimiento del contenido. Organización del dominio por categorías: cantidad, incertidumbre y datos, cambio y relaciones, y espacio y forma.
- Proceso cognitivo. Razonamiento matemático y ciclo de resolución de problemas: formulación, empleo e interpretación y evaluación.
- Contexto. Situaciones de la vida real en las que se ubican las preguntas, además de habilidades seleccionadas para el siglo XXI que se sustentan y se desarrollan a través de la competencia matemática: personal, ocupacional, social y científico.
Por lo tanto, se observa la adquisición de la competencia matemática de los alumnos con una secuencia sistematizada de actividades que articulan el conocimiento (saberes) y los procesos (competencias específicas). Además, han de tener lugar en un contexto de la vida real o basarse en situaciones ficticias pero verosímiles, en las que las matemáticas puedan aplicarse para resolver los problemas.
Ejemplo de pregunta matemática en PISA 2022
Ahora que sabemos la teoría, vamos a la práctica. Analicemos los aspectos de esta pregunta de patrón de triángulos de la prueba de matemáticas de PISA 2022:
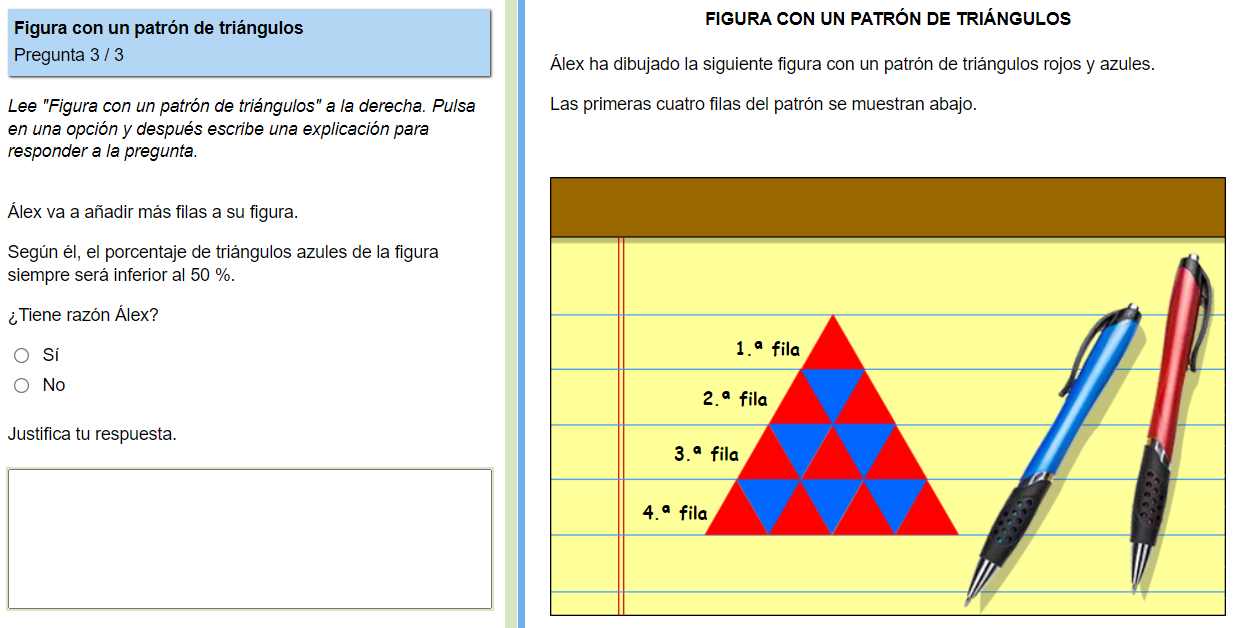
- Área de conocimiento: cambio y relaciones, sentido algebraico Patrones.
- Proceso cognitivo: razonamiento, requiere que los alumnos formulen y comprueben conjeturas sencillas analizando el patrón (competencia específica matemática 3) para reconocer la relación entre el número de triángulos rojos y azules en cada fila, y utilicen esta relación para justificar la respuesta.
- Contexto: científico, ya que todos los elementos pertenecen al ámbito matemático.
Ejemplo de actividad en ONMAT
Todas las actividades de ONMAT contienen información pedagógica detallada sobre los mismos aspectos que encontramos en las preguntas de PISA.
En esta actividad de ONMAT para 3.er curso de secundaria es equivalente a la pregunta de patrón de triángulos de PISA, ya que se trabajan los mismos aspectos:
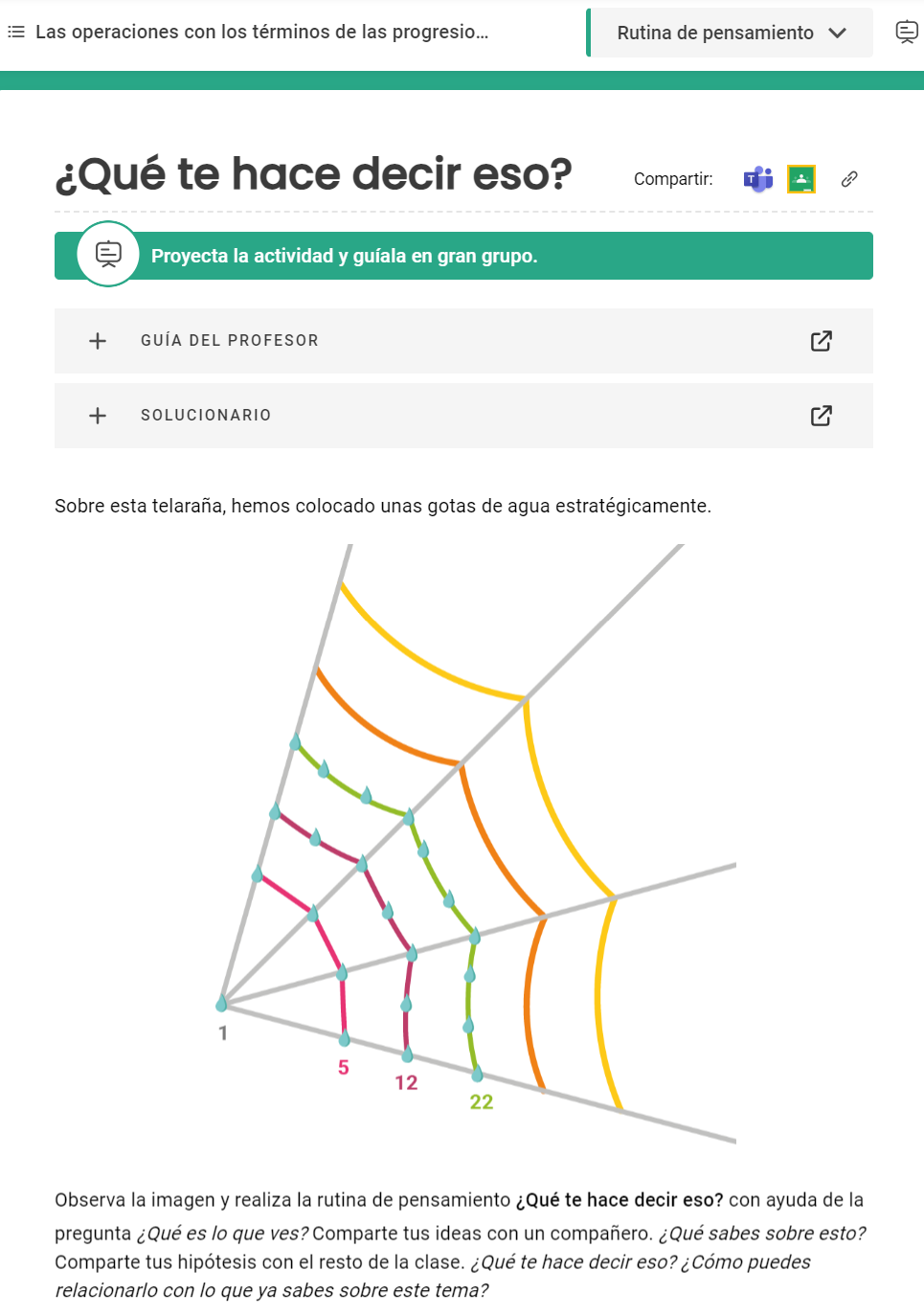
- Área de conocimiento (saberes): cambio y relaciones, sentido algebraico Patrones.
- Proceso cognitivo (competencias y criterios): rutina de razonamiento que requiere que los alumnos formulen y comprueben conjeturas sencillas de forma guiada analizando el patrón de gotas de agua de la telaraña (competencia específica matemática 3).
- Contexto: científico, aplicado al mundo natural.
Evaluación competencial: practica las pruebas PISA en ONMAT
ONMAT ofrece recursos, actividades, ejercicios e instrumentos de evaluación secuenciados que permiten un aprendizaje competencial e infinidad de momentos para que el docente lo pueda observar y evaluar.
Una enseñanza competencial solo está completa si la evaluación también es competencial. A lo largo de los 4 cursos de la ESO, ONMAT integra distintas herramientas de evaluación y autoevaluación para valorar el nivel de competencia matemática de los alumnos.
En ONMAT, los estudiantes pueden prepararse directamente para las PISA con pruebas autocorregibles en formato idéntico a las oficiales, ya que la plataforma recoge las actividades y exámenes de ediciones anteriores. ¡Te animamos a probarlas en el aula!
¿Quieres saber más sobre cómo aplicar la enseñanza competencial en tus clases de matemáticas? Contacta con nosotros y el equipo de asesores pedagógicos te mostrará las estrategias y herramientas de los programas EMAT y ONMAT.
También te invitamos a probar gratis la plataforma de ONMAT.
¡Descubre todos los contenidos!

















