L’ensenyament de les matemàtiques sempre ha estat una qüestió educativa complexa, que a més té una dificultat afegida quan treballem a secundària amb adolescents. En una etapa de grans canvis i reptes, és comú que els alumnes puguin sentir desmotivació o desinterès per algunes assignatures, circumstància que, per descomptat, afecta les matemàtiques. En aquest article, explorarem les raons per les quals els adolescents poden tenir dificultats per a motivar-se dins l’aula de matemàtiques, així com algunes estratègies que poden ajudar a fomentar el seu interès i compromís amb aquesta matèria.
3 consells per dissenyar demostracions matemàtiques que assegurin l’aprenentatge
Una de las causes que poden explicar el desinterès dels adolescents per les matemàtiques és que aquestes són un llenguatge abstracte. Ja ens ho indica la RAE quan diu que són una «ciència deductiva que estudia les propietats dels ens abstractes, com números, figures geomètriques o símbols, i les seves relacions». Així doncs, és important entendre que la pròpia naturalesa abstracta de les matemàtiques pot ser difícil d’assimilar per a un adolescent, ja que els números, les formes i els símbols no es veuen… o sí?
És en aquesta cruïlla on apareixen les demostracions matemàtiques, que molts experts en didàctica coincideixen que s’han de treballar com una estratègia central per ensenyar matemàtiques a secundària, ja que ajuda els alumnes a treballar de forma ordenada i sistemàtica i fomenta la seva capacitat de raonament matemàtic. En què s’han de basar, doncs, aquestes demostracions per assegurar que es comprenen (i a posteriori es consoliden) el conceptes?
1. Anar de quelcom simple a quelcom complex
Si comencem introduint conceptes simples i construint de forma gradual sobre aquests conceptes més difícils, els alumnes poden desenvolupar una comprensió profunda i significativa de les matemàtiques. Aquesta estratègia ajuda també als adolescents a sentir-se més còmodes i segurs amb la matèria a mesura que avancen cap a nocions matemàtiques més desafiadores. Així mateix, anar de quelcom simple a quelcom complex pot fomentar la seva curiositat i motivació perquè se’ls dona l’oportunitat de descobrir com els coneixements matemàtics es relacionen entre si i com s’apliquen a situacions del món real.
2. Relacionar els coneixements entre si
Un concepte matemàtic no existeix en el buit, sinó que està interconnectat i permet la construcció (i connexió) de nous conceptes. Quan dins l’aula relacionem coneixements matemàtics entre si, els alumnes poden veure com els conceptes s’enllacen i com poden aplicar-se en diferents àrees de les matemàtiques. Aquesta estratègia ajuda també a identificar patrons dins els conceptes, el que els ajuda, en primera instància, a millorar la seva capacitat per resoldre problemes de manera efectiva i creativa, alhora que fomenta i desenvolupa les seves habilitats de pensament crític.
3. Conèixer quins són els coneixements que són requisits previs per a altres coneixements
Haurem de tenir en compte els diferents nivells de coneixement que tenen els alumnes dins l’aula per introduir nous conceptes, i no donar per descomptat que hi ha coneixements que ja tenen assimilats «perquè és el que toca a la seva edat». Per això, és important realitzar una avaluació inicial dels coneixements que té l’alumnat, per poder adaptar la proposta didàctica i impedir que hi hagi alumnes que es queden enrere i es desmotiven. A ONMAT, per exemple, oferim accés a totes les activitats de tots els cursos de secundària, a més de a totes les activitats de 6è de primària, per si fos necessari refrescar conceptes.
Vols aprofundir més en les demostracions matemàtiques?
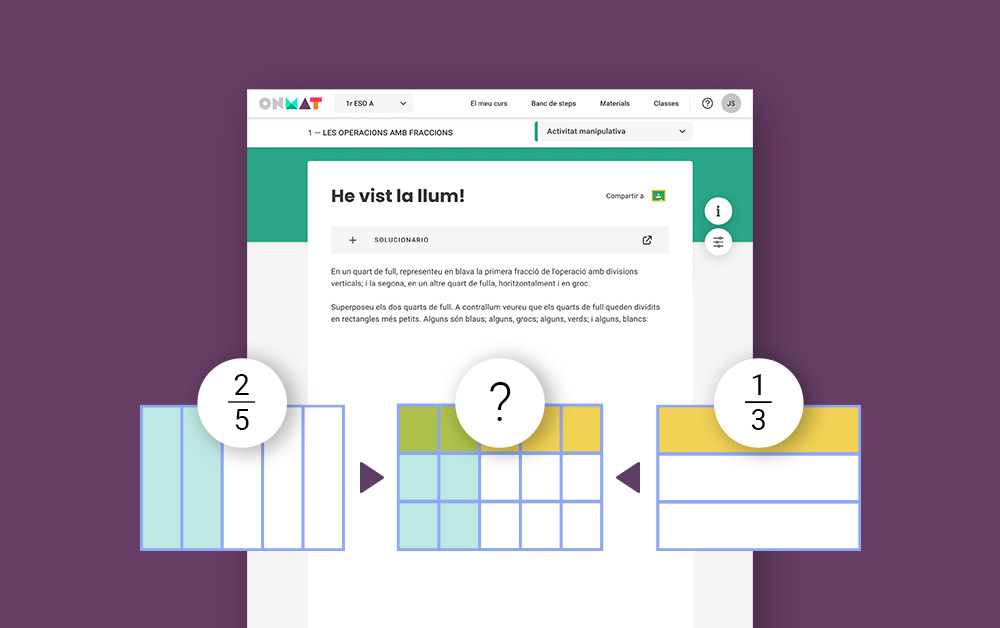
A tekman creiem en la importància de treballar demostracions matemàtiques dins l’aula, i és per això que el nostre programa ONMAT es fonamenta en activitats amb demostracions matemàtiques visuals, lúdiques i manipulatives, perquè els teus alumnes gaudeixin aprenent mentre adquireixen les competències matemàtiques.
Mira aquest webinar on els nostres especialistes en didàctica de les matemàtiques ens van ensenyar nombrosos exemples i estratègies de com introduir les demostracions matemàtiques dins l’aula per construir un coneixement significatiu i durador.
A més, t’hem preparat una completa guia amb diverses estratègies i demostracions matemàtiques que t’ajudaran a aconseguir que els teus alumnes interioritzin conceptes matemàtics complexos i abstractes a través d’activitats manipulatives i de rutines de pensament.